Do celu
Badanie energii kinetycznej na podstawie ruchu o zmiennej prędkości.

Włącz się
(Przed zajęciami (20 min))
– Te zajęcia dotyczą sposobu, w jaki energia kinetyczna związana jest z prędkością i masą. Uczniowie przeprowadzą doświadczenie dotyczące mierzenia odległości przebytej w czasie. Danymi wejściowymi będzie liczba obrotów koła. Na podstawie wykresu przedstawiającego liczbę obrotów koła w czasie przygotują wykres prezentujący odległość przebytą w czasie, a następnie spróbują przedstawić również zmiany prędkości w czasie. Na koniec obliczą energię kinetyczną, podstawiając maksymalną prędkość do poniższego wzoru: Ek = ½mv2 m = 305 g
– Wykorzystaj różne materiały, by zaangażować uczniów w rozmowę na temat energii kinetycznej.
Dyskusja
Rozpocznij dyskusję, zadając pytania związane z zajęciami. Oto kilka propozycji:
– Jak wygląda wykres przedstawiający odległość przebytą w czasie?
– Jak wygląda wykres przedstawiający zmiany prędkości w czasie?
– Jak wygląda wykres przedstawiający zmiany energii kinetycznej w czasie?
Poproś uczniów o zapisanie ich przemyśleń w formie hipotezy.
Wymyśl
(Podczas zajęć (30 min))
– Poproś uczniów o zbudowanie pojazdu ze swobodnie poruszającymi się kołami, który będzie zliczał obroty kół. Uczniowie mogą zbudować własny model lub model Kamień curlingowy według instrukcji budowania w aplikacji.
– Poproś uczniów o przetestowanie modeli za pomocą sugerowanego programu.
– Poproś uczniów o narysowanie wykresu przedstawiającego odległość przebytą w czasie i opisanie go:
– Co oznaczają gwałtowne wzrosty i spadki na wykresie?
– Dlaczego z czasem odległość między nimi się zwiększa?
Wytłumacz
(Podczas zajęć (15 min))
– Poproś uczniów o kontynuowanie doświadczenia poprzez:
– przekształcenie liczby obrotów na sekundę na odległość,
– przekształcenie odległości przebytej w czasie na prędkość.
– Daj uczniom czas na dostosowanie programów i ulepszenie ich wydajności.
– Zachęć ich do rejestrowania jak największej liczby danych podczas przeprowadzania doświadczeń.
– Poproś uczniów o wyeksportowanie danych w pliku CSV, który można w razie potrzeby edytować w innych programach.
Weryfikuj
(Po zajęciach (20 min))
– Jeśli uczniowie nadal mają dostęp do zestawów SPIKE Prime, poproś ich o wykonanie zadań z aplikacji SPIKE, które rozwiną ich wiedzę praktyczną, na przykład:
– Uczniowie mogą zagrać w grę i zapisać swoje wyniki. Poproś uczniów o popychanie kamieni curlingowych w taki sposób, aby przód modelu zatrzymał się jak najbliżej środka celu. Wyjaśnij, że każdy uczeń może spróbować trzy razy i po każdej próbie powinien zmierzyć odległość od środka celu do przodu modelu. Grę wygrywa uczeń lub zespół z najmniejszą łączną odległością po trzech próbach.
– Jeśli uczniowie nie mają dostępu do zestawów, poproś ich o uzupełnienie Notatnika wynalazcy lub zadaj im do wykonania jedno z zaproponowanych niżej ćwiczeń rozwijających umiejętności. Większość z ćwiczeń rozwijających umiejętności można wykonać za pomocą danych zgromadzonych podczas sesji zajęć praktycznych.
– Poprowadź sesję, podczas której uczniowie będą wymieniać informacje miedzy sobą. Sesję można przeprowadzić za pomocą dowolnych, najskuteczniejszych metod lub narzędzi (np. w klasie lub online).
Ocena
– Przekaż każdemu uczniowi opinię na temat jego pracy.
– Aby uprościć ten proces, możesz skorzystać z podanych kryteriów oceny.
Możliwości oceny
Lista kontrolna obserwacji nauczyciela
Przygotuj odpowiednią skalę, na przykład:
– Częściowo zrealizowane
– Całkowicie zrealizowane
– Powyżej oczekiwań
Aby ocenić postępy uczniów, wykorzystaj następujące kryteria:
– Uczniowie potrafią zaprogramować urządzenie do zapisywania danych na wykresie liniowym.
– Uczniowie potrafią interpretować wartości przedstawione na wykresie liniowym.
– Uczniowie potrafią wyjaśnić energię kinetyczną w odniesieniu do prędkości.
Samoocena
Poproś uczniów o wybranie klocków, które ich zdaniem najlepiej reprezentują ich pracę.
– Niebieski: potrafię narysować wykres z danymi za pomocą programu podanego w aplikacji.
– Żółty: potrafię narysować własny wykres liniowy i wyjaśnić swoje wyniki.
– Fioletowy: potrafię samodzielnie przygotować nowe doświadczenie.
Opinie o pracy koleżanek i kolegów
Zachęć uczniów, aby dzielili się opiniami na temat innych w następujący sposób:
– Niech wzajemnie oceniają swoją pracę na powyższej kolorowej skali z klocków.
– Niech wyrażają konstruktywne opinie o pracy innych, tak aby podczas kolejnej lekcji osiągnęli lepsze wyniki. To dobra okazja do wykorzystania narzędzi do wideokonferencji lub postów na blogu w scenariuszu nauczania mieszanego.

Zróżnicowanie
Jeśli chcesz, aby lekcja była łatwiejsza:
– Ogranicz zajęcia w taki sposób, by uczniowie skupili się tylko na zmianach odległości przebytej w czasie.
Jeśli chcesz, aby lekcja była trudniejsza:
– Poproś uczniów, aby zaprojektowali i zbudowali własne pojazdy bez silnika oraz kamienie curlingowe, powtórzyli doświadczenie i porównali dane z wynikami innych modeli (np. z danymi uzyskanymi przez innego ucznia).
– Poproś uczniów, aby zaprojektowali i zbudowali własne urządzenia do pchania, które umożliwią popychanie w bardziej regularny sposób, oraz aby udokumentowali proces projektowy.

Wskazówki
Wskazówki dotyczące budowania

Wskazówki dotyczące programowania
Ta lekcja jest przeznaczona do odtworzenia, gdy Hub jest podłączony przez USB lub Bluetooth. Po połączeniu dane gromadzone przez Hub są przesyłane bezpośrednio na urządzenie i umieszczane na wykresie liniowym w czasie rzeczywistym.
Program główny

Program rozwiązań

Wskazówki dotyczące danych
Oto przykładowe dane, jakie uczniowie mogą uzyskać podczas tego doświadczenia.
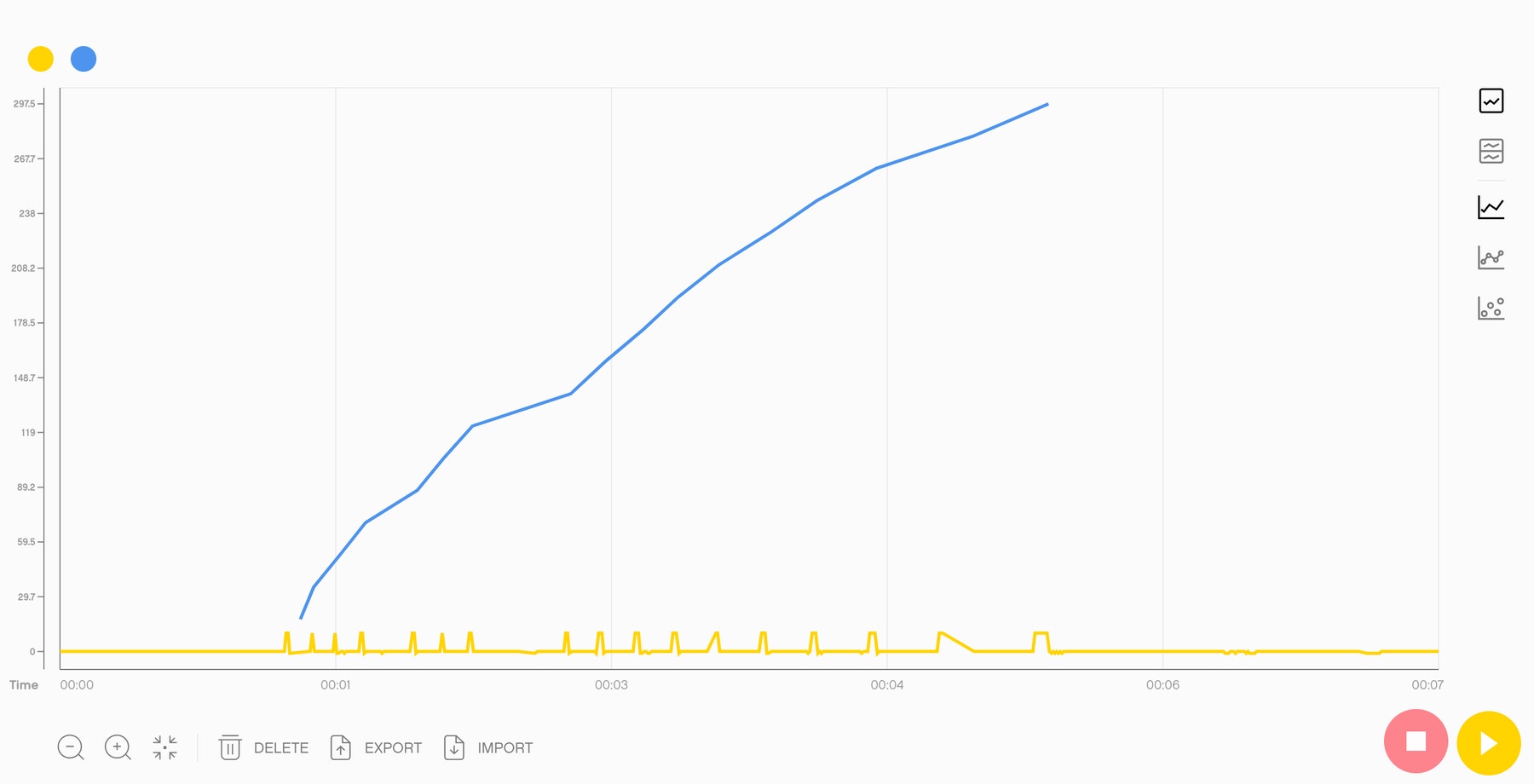
Rozwój umiejętności
Rozwój umiejętności matematycznych
Aby dodatkowo rozwijać umiejętności matematyczne:
– Poproś uczniów o sprawdzenie, co się stanie, gdy zmienią masę kamienia curlingowego poprzez dodanie innych elementów LEGO (np. silników) albo ciężkich przedmiotów (np. butelki z wodą). Poproś ich o zaktualizowanie modeli, ponowne przeprowadzenie doświadczenia i porównanie wykresów przedstawiających prędkość w czasie dla różnych mas.
Uwaga: potrzebny będzie dodatkowy czas.

Rozwój umiejętności językowych
Aby dodatkowo rozwijać umiejętności językowe:
– Poproś uczniów o przygotowanie kampanii marketingowej reklamującej główne cechy ich modelu. Kampania powinna zawierać dane techniczne modelu i przedstawiać fakty naukowe związane z prędkością i energią, które podkreślą zalety modelu.
Uwaga: potrzebny będzie dodatkowy czas.

Powiązanie z przyszłym zawodem
Uczniowie, którym podobała się ta lekcja, mogą być zainteresowani pracą zawodową w następujących dziedzinach:
– Edukacja i szkolenia
– Nauki medyczne
Wsparcie dla nauczyciela
Uczniowie:
– Obliczą początkową prędkość zwalniającego ruchu na podstawie wykresu liniowego przedstawiającego odległość przebytą w czasie.
– Na podstawie tej przybliżonej prędkości obliczą średnią energię kinetyczną.
Zestaw LEGO® Education SPIKE™ Prime
Urządzenie z zainstalowaną aplikacją LEGO Education SPIKE
Fizyka
Uczeń:
• 1.1 wyodrębnia z tekstów, tabel, diagramów lub wykresów, rysunków schematycznych lub blokowych informacje kluczowe dla opisywanego zjawiska bądź problemu; ilustruje je w różnych postaciach;
• 1.2 wyodrębnia zjawisko z kontekstu, nazywa je oraz wskazuje czynniki istotne i nieistotne dla jego przebiegu;
• 1.3 rozróżnia pojęcia: obserwacja, pomiar, doświadczenie; przeprowadza wybrane obserwacje, pomiary i doświadczenia korzystając z ich opisów;
• 1.4 opisuje przebieg doświadczenia lub pokazu; wyróżnia kluczowe kroki i sposób postępowania oraz wskazuje rolę użytych przyrządów;
• 1.6 przeprowadza obliczenia i zapisuje wynik zgodnie z zasadami zaokrąglania oraz zachowaniem liczby cyfr znaczących wynikającej z dokładności pomiaru lub z danych;
• 1.8 rozpoznaje zależność rosnącą bądź malejącą na podstawie danych z tabeli lub na podstawie wykresu; rozpoznaje proporcjonalność prostą na podstawie wykresu;
• 2.1 opisuje i wskazuje przykłady względności ruchu;
• 2.2 wyróżnia pojęcia tor i droga;
• 2.3 przelicza jednostki czasu (sekunda, minuta, godzina);
• 2.4 posługuje się pojęciem prędkości do opisu ruchu prostoliniowego; oblicza jej wartość i przelicza jej jednostki; stosuje do obliczeń związek prędkości z drogą i czasem, w którym została przebyta;
• 2.5 nazywa ruchem jednostajnym ruch, w którym droga przebyta w jednostkowych przedziałach czasu jest stała;
• 2.6 wyznacza wartość prędkości i drogę z wykresów zależności prędkości i drogi od czasu dla ruchu prostoliniowego odcinkami jednostajnego oraz rysuje te wykresy na podstawie podanych informacji;
• 2.7 nazywa ruchem jednostajnie przyspieszonym ruch, w którym wartość prędkości rośnie w jednostkowych przedziałach czasu o tę samą wartość, a ruchem jednostajnie opóźnionym – ruch, w którym wartość prędkości maleje w jednostkowych przedziałach czasu o tę samą wartość;
• 2.8 posługuje się pojęciem przyspieszenia do opisu ruchu prostoliniowego jednostajnie przyspieszonego i jednostajnie opóźnionego; wyznacza wartość przyspieszenia wraz z jednostką; stosuje do obliczeń związek przyspieszenia ze zmianą prędkości i czasem, w którym ta zmiana nastąpiła (Δv = a·Δt);
• 2.9 wyznacza zmianę prędkości i przyspieszenie z wykresów zależności prędkości od czasu dla ruchu prostoliniowego jednostajnie zmiennego (przyspieszonego lub opóźnionego);
• 3.3 posługuje się pojęciem energii kinetycznej, potencjalnej grawitacji i potencjalnej sprężystości; opisuje wykonaną pracę jako zmianę energii;
• 3.4 wyznacza zmianę energii potencjalnej grawitacji oraz energii kinetycznej;
• 3.5 wykorzystuje zasadę zachowania energii do opisu zjawisk oraz zasadę zachowania energii mechanicznej do obliczeń.
Matematyka
Uczeń:
• 3.1 zapisuje wyniki podanych działań w postaci wyrażeń algebraicznych jednej lub kilku zmiennych;
• 3.2 oblicza wartości liczbowe wyrażeń algebraicznych;
• 3.3 zapisuje zależności przedstawione w zadaniach w postaci wyrażeń algebraicznych jednej lub kilku zmiennych;
• 4.1 porządkuje jednomiany i dodaje jednomiany podobne (tzn. różniące się jedynie współczynnikiem liczbowym);
• 4.2 dodaje i odejmuje sumy algebraiczne, dokonując przy tym redukcji wyrazów podobnych;
• 6.2 rozwiązuje równania pierwszego stopnia z jedną niewiadomą metodą równań równoważnych;
• 6.5 przekształca proste wzory, aby wyznaczyć zadaną wielkość we wzorach geometrycznych (np. pól figur) i fizycznych (np. dotyczących prędkości, drogi i czasu).
• 10.2 znajduje współrzędne danych (na rysunku) punktów kratowych w układzie współrzędnych na płaszczyźnie;
• 10.3 rysuje w układzie współrzędnych na płaszczyźnie punkty kratowe o danych współrzędnych całkowitych (dowolnego znaku);
• 13.1 interpretuje dane przedstawione za pomocą tabel, diagramów słupkowych i kołowych, wykresów, w tym także wykresów w układzie współrzędnych;
• 13.2 tworzy diagramy słupkowe i kołowe oraz wykresy liniowe na podstawie zebranych przez siebie danych lub danych pochodzących z różnych źródeł;14.1
Język polski
Uczeń:
• 3.1.2 gromadzi i porządkuje materiał rzeczowy potrzebny do tworzenia wypowiedzi; redaguje plan kompozycyjny własnej wypowiedzi;
• 3.1.3 tworzy wypowiedź, stosując odpowiednią dla danej formy gatunkowej kompozycję oraz zasady spójności językowej między akapitami; rozumie rolę akapitów jako spójnych całości myślowych w tworzeniu wypowiedzi pisemnych oraz stosuje rytm akapitowy (przeplatanie akapitów dłuższych i krótszych);
• 3.1.4 wykorzystuje znajomość zasad tworzenia tezy i hipotezy oraz argumentów przy tworzeniu rozprawki oraz innych tekstów argumentacyjnych;
• 3.1.6 przeprowadza wnioskowanie jako element wywodu argumentacyjnego;
• 4.1 rzetelnie, z poszanowaniem praw autorskich, korzysta z informacji;
• 4.4 uczestniczy w projektach edukacyjnych (np. tworzy różnorodne prezentacje, projekty wystaw, realizuje krótkie filmy z wykorzystaniem technologii multimedialnych);
• 4.6 rozwija umiejętności samodzielnej prezentacji wyników swojej pracy;
• 4.8 rozwija umiejętność krytycznego myślenia i formułowania opinii.
Materiały dla uczniów
Arkusz dla ucznia
Download, view or share the student worksheet, either as an online HTML page or a printable PDF