Tor przeszkód
Ilustrowanie konwersji energii potencjalnej i kinetycznej.

Włącz się
(Część A projektu, przed zajęciami (30 min))
– Podczas tych zajęć uczniowie wykorzystają to, czego już się nauczyli o energii potencjalnej i kinetycznej. Będą postępować zgodnie z procesem projektowania inżynieryjnego i wykonają otwarty projekt polegający na zbudowaniu toru przeszkód, który zademonstruje, na ile opanowali te zagadnienia.
– Do tego projektu najlepiej pasują przeszkody wykorzystujące wahadło, huśtawkę oraz inne urządzenia poruszające się w górę i w dół.
– Wykorzystaj różne materiały, aby zaangażować uczniów w rozmowę na temat wartości kątów RPY (pochylenia, obrotu i odchylenia)* .
Dyskusja
Rozpocznij dyskusję, zadając pytania związane z zajęciami. Oto kilka propozycji:
– W jaki sposób energia kinetyczna i potencjalna są ze sobą powiązane?
– Czy znasz jakieś gry i zabawy wykorzystujące tor przeszkód?
Poproś uczniów o zapisanie ich przemyśleń w formie hipotezy.
Wymyśl
(Część A projektu, podczas zajęć (45 min))
– Poproś uczniów, aby w parach przeprowadzili burzę mózgów i wymyślili dwie lub trzy przeszkody na tor przeszkód.
– Poproś, aby wymyślili, jak rejestrować w nich wartości w celu zilustrowania konwersji energii.
– W swoich pomysłach uczniowie powinni wziąć pod uwagę wykorzystanie danych.
– Daj uczniom czas na zbudowanie prototypów.
Wytłumacz
(Część B projektu, podczas zajęć (45 min))
– Poproś uczniów o przeprowadzenie doświadczeń.
– Zachęć ich do rejestrowania dużej ilości danych do późniejszego wykorzystania. Poproś ich również o opisanie wartości, które będą zapisywane na wykresach.
– Poproś uczniów o nagranie filmów z testowania modeli.
Weryfikuj
(Część B projektu, po zajęciach (45 min))
– Poprowadź sesję, podczas której uczniowie będą wymieniać informacje miedzy sobą. Sesję można przeprowadzić za pomocą dowolnych, najskuteczniejszych metod lub narzędzi (np. w klasie lub online).
Ocena
– Przekaż każdemu uczniowi opinię na temat jego pracy.
– Aby uprościć ten proces, możesz skorzystać z podanych kryteriów oceny.
Możliwości oceny
Lista kontrolna obserwacji nauczyciela
Przygotuj odpowiednią skalę, na przykład:
– Częściowo zrealizowane
– Całkowicie zrealizowane
– Powyżej oczekiwań
Aby ocenić postępy uczniów, wykorzystaj następujące kryteria:
– Uczniowie potrafią zidentyfikować kluczowe elementy problemu.
– Uczniowie potrafią pracować niezależnie, aby opracować pomysłowe, działające rozwiązanie.
– Uczniowie potrafią jasno przedstawiać swoje pomysły.
Samoocena
Poproś uczniów o wybranie klocków, które ich zdaniem najlepiej reprezentują ich pracę.
– Niebieski: udało mi się zbudować model toru przeszkód.
– Żółty: udało mi się zbudować model toru przeszkód i zarejestrować dane ilustrujące konwersję energii.
– Fioletowy: udało mi się zbudować model toru przeszkód. Udało mi się również zarejestrować dane ilustrujące konwersję energii i w jasny sposób przedstawić swoje pomysły.
Opinie o pracy koleżanek i kolegów
Zachęć uczniów, aby dzielili się opiniami na temat innych w następujący sposób:
– Niech wzajemnie oceniają swoją pracę na powyższej kolorowej skali z klocków.
– Niech wyrażają konstruktywne opinie o pracy innych, tak aby podczas kolejnej lekcji jako grupa osiągnęli lepsze wyniki.

Zróżnicowanie
Jeśli chcesz, aby lekcja była łatwiejsza:
– Pokaż uczniom cztery lub pięć przykładowych przeszkód, z których mogą wybrać jedną do zbudowania. Przykładowe modele:
– Przeszkoda z drążkiem gimnastycznym
– Przeszkoda z kółkami gimnastycznymi
– Przeszkoda z liną do zjazdów
– Przeszkoda z drabiną
– Na przykładzie modelu Przeszkoda z drążkiem gimnastycznym pokaż uczniom, co będą robić.
Jeśli chcesz, aby lekcja była trudniejsza:
– Poprowadź burzę mózgów w całej klasie, aby grupy miały więcej pomysłów do wyboru.
– Poproś uczniów o podzielenie się pomysłami na przeszkody albo na wykorzystanie silnika i czujników.

Wskazówki
Wskazówki dotyczące budowania
Rozwiązania otwarte
Ten projekt opracowano w taki sposób, aby każdy uczeń lub zespół mógł wymyślić wyjątkowe rozwiązanie.
Przykładowe rozwiązanie
Oto pomysł, który możesz wykorzystać, aby zainspirować uczniów w procesie projektowania.

Wskazówki dotyczące programowania
Program główny

Wskazówki dotyczące danych
Oto przykładowe dane, jakie uczniowie mogą uzyskać podczas tego doświadczenia.
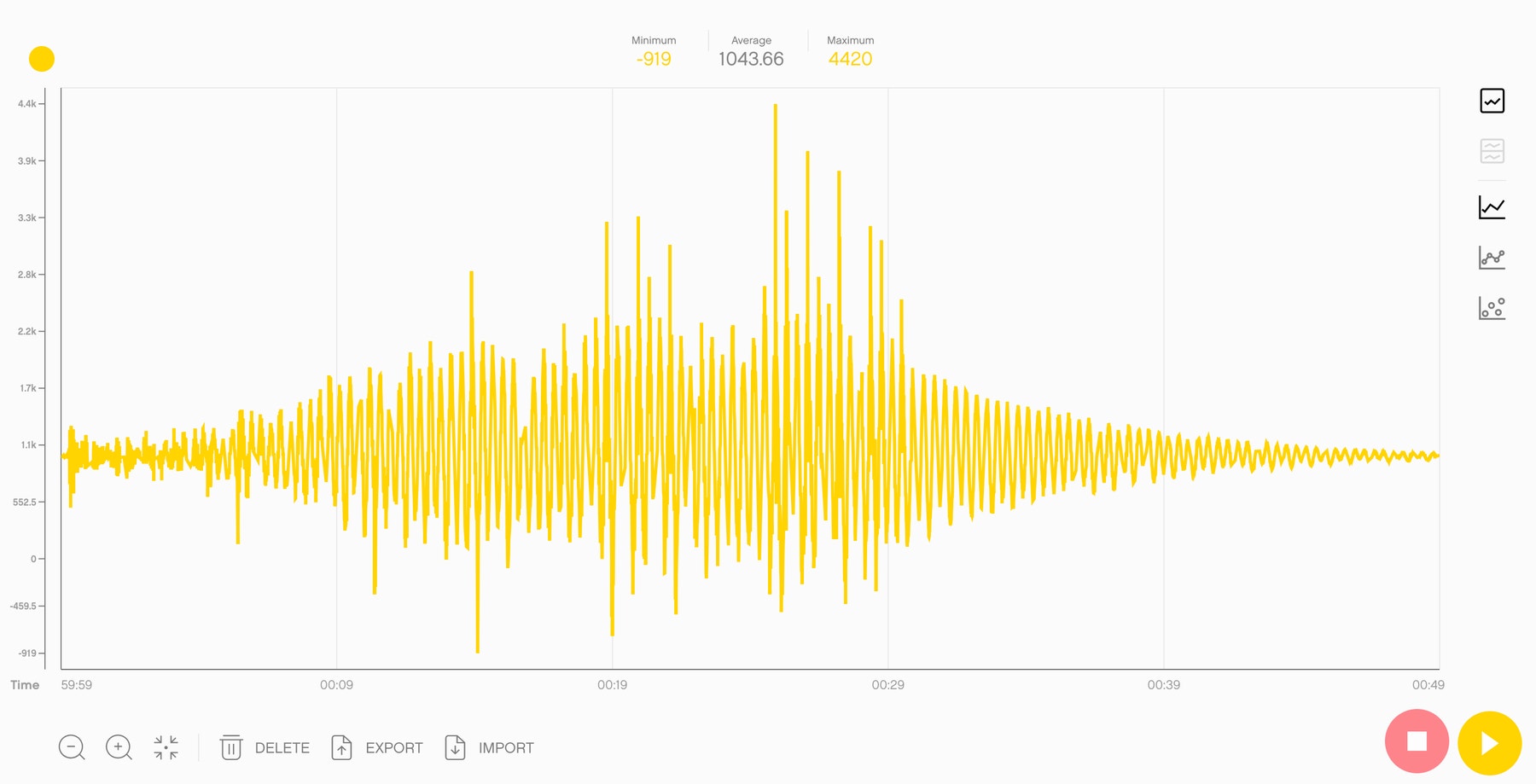
Rozwój umiejętności
Rozwój umiejętności matematycznych
Aby dodatkowo rozwijać umiejętności matematyczne:
– Poproś uczniów wykorzystanie Hubów do rejestrowania danych poza klasą. Mogą na przykład zarejestrować wartości przyspieszenia w windzie, na placu zabaw lub w parku rozrywki. Poproś ich o porównanie i opisanie wykresów z każdego miejsca.
Uwaga: potrzebny będzie dodatkowy czas.

Rozwój umiejętności językowych
Aby dodatkowo rozwijać umiejętności językowe:
– Podziel grupy uczniów w pary podczas fazy Weryfikuj. Jedna grupa prezentuje swój model, a druga robi notatki, zadaje pytania i przeprowadza wywiad. Następnie grupy zamieniają się rolami. Gdy obie grupy zaprezentują swoje modele, przygotowują post na bloga albo film o tym, czego dowiedziały się o modelu drugiej grupy.
Uwaga: potrzebny będzie dodatkowy czas.

Powiązanie z przyszłym zawodem
Uczniowie, którym podobała się ta lekcja, mogą być zainteresowani pracą zawodową w następujących dziedzinach:
– Usługi terapeutyczne
– Inżynieria i technologia
Wsparcie dla nauczyciela
Uczniowie:
– Zbudują model toru przeszkód ilustrujący wykorzystanie energii potencjalnej i kinetycznej.
Zestaw LEGO® Education SPIKE™ Prime
Urządzenie z zainstalowaną aplikacją LEGO Education SPIKE
Dowolne inne materiały związane z projektem
Fizyka
Uczeń:
• 1.1 wyodrębnia z tekstów, tabel, diagramów lub wykresów, rysunków schematycznych lub blokowych informacje kluczowe dla opisywanego zjawiska bądź problemu; ilustruje je w różnych postaciach;
• 1.2 wyodrębnia zjawisko z kontekstu, nazywa je oraz wskazuje czynniki istotne i nieistotne dla jego przebiegu;
• 1.3 rozróżnia pojęcia: obserwacja, pomiar, doświadczenie; przeprowadza wybrane obserwacje, pomiary i doświadczenia korzystając z ich opisów;
• 1.4 opisuje przebieg doświadczenia lub pokazu; wyróżnia kluczowe kroki i sposób postępowania oraz wskazuje rolę użytych przyrządów;
• 1.6 przeprowadza obliczenia i zapisuje wynik zgodnie z zasadami zaokrąglania oraz zachowaniem liczby cyfr znaczących wynikającej z dokładności pomiaru lub z danych;
• 1.8 rozpoznaje zależność rosnącą bądź malejącą na podstawie danych z tabeli lub na podstawie wykresu; rozpoznaje proporcjonalność prostą na podstawie wykresu;
• 2.1 opisuje i wskazuje przykłady względności ruchu;
• 2.2 wyróżnia pojęcia tor i droga;
• 2.3 przelicza jednostki czasu (sekunda, minuta, godzina);
• 2.4 posługuje się pojęciem prędkości do opisu ruchu prostoliniowego; oblicza jej wartość i przelicza jej jednostki; stosuje do obliczeń związek prędkości z drogą i czasem, w którym została przebyta;
• 2.5 nazywa ruchem jednostajnym ruch, w którym droga przebyta w jednostkowych przedziałach czasu jest stała;
• 2.6 wyznacza wartość prędkości i drogę z wykresów zależności prędkości i drogi od czasu dla ruchu prostoliniowego odcinkami jednostajnego oraz rysuje te wykresy na podstawie podanych informacji;
• 2.7 nazywa ruchem jednostajnie przyspieszonym ruch, w którym wartość prędkości rośnie w jednostkowych przedziałach czasu o tę samą wartość, a ruchem jednostajnie opóźnionym – ruch, w którym wartość prędkości maleje w jednostkowych przedziałach czasu o tę samą wartość;
• 2.8 posługuje się pojęciem przyspieszenia do opisu ruchu prostoliniowego jednostajnie przyspieszonego i jednostajnie opóźnionego; wyznacza wartość przyspieszenia wraz z jednostką; stosuje do obliczeń związek przyspieszenia ze zmianą prędkości i czasem, w którym ta zmiana nastąpiła (Δv = a·Δt);
• 2.9 wyznacza zmianę prędkości i przyspieszenie z wykresów zależności prędkości od czasu dla ruchu prostoliniowego jednostajnie zmiennego (przyspieszonego lub opóźnionego);
• 3.3 posługuje się pojęciem energii kinetycznej, potencjalnej grawitacji i potencjalnej sprężystości; opisuje wykonaną pracę jako zmianę energii;
• 3.4 wyznacza zmianę energii potencjalnej grawitacji oraz energii kinetycznej;
• 3.5 wykorzystuje zasadę zachowania energii do opisu zjawisk oraz zasadę zachowania energii mechanicznej do obliczeń.
Matematyka
Uczeń:
• 10.2 znajduje współrzędne danych (na rysunku) punktów kratowych w układzie współrzędnych na płaszczyźnie;
• 10.3 rysuje w układzie współrzędnych na płaszczyźnie punkty kratowe o danych współrzędnych całkowitych (dowolnego znaku);
• 13.1 interpretuje dane przedstawione za pomocą tabel, diagramów słupkowych i kołowych, wykresów, w tym także wykresów w układzie współrzędnych;
• 13.2 tworzy diagramy słupkowe i kołowe oraz wykresy liniowe na podstawie zebranych przez siebie danych lub danych pochodzących z różnych źródeł;
Język polski
Uczeń:
• 3.1.2 gromadzi i porządkuje materiał rzeczowy potrzebny do tworzenia wypowiedzi; redaguje plan kompozycyjny własnej wypowiedzi;
• 3.1.3 tworzy wypowiedź, stosując odpowiednią dla danej formy gatunkowej kompozycję oraz zasady spójności językowej między akapitami; rozumie rolę akapitów jako spójnych całości myślowych w tworzeniu wypowiedzi pisemnych oraz stosuje rytm akapitowy (przeplatanie akapitów dłuższych i krótszych);
• 3.1.4 wykorzystuje znajomość zasad tworzenia tezy i hipotezy oraz argumentów przy tworzeniu rozprawki oraz innych tekstów argumentacyjnych;
• 3.1.6 przeprowadza wnioskowanie jako element wywodu argumentacyjnego;
• 3.2.1 tworzy spójne wypowiedzi w następujących formach gatunkowych: recenzja, rozprawka, podanie, życiorys, CV, list motywacyjny, przemówienie, wywiad;
• 3.2.3 formułuje pytania do tekstu;
• 4.1 rzetelnie, z poszanowaniem praw autorskich, korzysta z informacji;
• 4.4 uczestniczy w projektach edukacyjnych (np. tworzy różnorodne prezentacje, projekty wystaw, realizuje krótkie filmy z wykorzystaniem technologii multimedialnych);
• 4.6 rozwija umiejętności samodzielnej prezentacji wyników swojej pracy;
• 4.8 rozwija umiejętność krytycznego myślenia i formułowania opinii.
5 pomysłów i przykładów nauczania mieszanego przy użyciu modelu 5E
Materiały dla uczniów
Arkusz dla ucznia
Download, view or share the student worksheet, either as an online HTML page or a printable PDF